2.8. Molecular Statistical Mechanics

2.8. Molecular Statistical Mechanics#

Overview#

In molecular statistical mechanics, one often needs to calculate the partition function for each degree of freedom (translational, rotational, vibrational, and electronic) to derive thermodynamic properties. This section summarizes common formulas for partition functions of various molecular shapes, under the approximate (rigid-rotor/harmonic-oscillator) models. We use rotational temperatures \(\Theta_{\text{rot}}\) and vibrational temperatures \(\Theta_{\text{vib}}\), which convert molecular constants into energy units scaled by Boltzmann’s constant \(k_{\text{B}}\).

Rotational Symmetry#

The rotational partition function \(q_{\text{rot}}\) depends on:

The rotational constants (encoded by \(\Theta_{\text{rot},A}\), \(\Theta_{\text{rot},B}\), \(\Theta_{\text{rot},C}\), etc.).
The rotational symmetry number \(\sigma\).
The temperature \(T\).

Below is a summary table of approximate expressions for the rotational partition functions of rigid rotors in the high-temperature limit \(\bigl(T \gg \Theta_{\text{rot}}\bigr)\). Here, \(\Theta_{\text{rot}}\) and \(T\) are both expressed in Kelvin, making the ratio \(T/\Theta_{\text{rot}}\) dimensionless.

Table 8 Rotational Partition Functions of Rigid Rotors#
Molecular Class	Symmetry Number (\(\sigma\))	Rotational Partition Function (\(q_{\text{rot}}\))	Examples (\(\sigma\))
Heteronuclear Diatomic (Linear)	1	\(\frac{T}{\Theta_{\text{rot}}}\)	CO, NO, HF, HCl, etc.
Asymmetric Polyatomic (Linear)	1	\(\frac{T}{\Theta_{\text{rot}}}\)	HCN, N₂O, FCN, etc.
Homonuclear Diatomic (Linear)	2	\(\frac{T}{2\,\Theta_{\text{rot}}}\)	H₂, O₂, N₂, etc.
Symmetric Polyatomic (Linear)	2	\(\frac{T}{2\,\Theta_{\text{rot}}}\)	CO₂, CS₂, XeF₂
Spherical Top	12 for \(T_d\) or 24 for \(O_h\)	\(\frac{\sqrt{\pi}}{\sigma}\,\biggl(\frac{T}{\Theta_{\text{rot}}}\biggr)^{3/2}\)	CH₄, SiH₄, SF₆, etc.
Symmetric Top	Varies with symmetry	\(\frac{\sqrt{\pi}}{\sigma}\,\sqrt{\frac{T^3}{\Theta_{\text{rot},A}^2\,\Theta_{\text{rot},C}}}\)	C₆H₆ (\(\sigma=12\)), NH₃ (\(\sigma=3\)), XeF₄ (\(\sigma=8\)), etc.
Asymmetric Top	Varies with symmetry	\(\frac{\sqrt{\pi}}{\sigma}\,\sqrt{\frac{T^3}{\Theta_{\text{rot},A}\,\Theta_{\text{rot},B}\,\Theta_{\text{rot},C}}}\)	H₂O (\(\sigma=2\)), NO₂ (\(\sigma=2\)), SO₂ (\(\sigma=2\)), most large molecules

Nonlinear Rigid Rotors#

Below is a visualization illustrating spherical top, symmetric top, and asymmetric top molecules. The semi-axes of each ellipsoid are scaled by \(\sqrt{\Theta_{\text{rot}, i}}\), emphasizing how the different principal rotational constants (or equivalently, rotational temperatures) define the 3D shape of the “rotational profile.”

Show code cell source Hide code cell source

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from myst_nb import glue

u = np.linspace(0, 2*np.pi, 100)
v = np.linspace(0, np.pi, 100)
u, v = np.meshgrid(u, v)

def surface_points(a, b, c):
    """Return x, y, z for an ellipsoid with semi-axes a, b, c."""
    x = a * np.cos(u) * np.sin(v)
    y = b * np.sin(u) * np.sin(v)
    z = c * np.cos(v)
    return x, y, z

# Rotational temperatures (sample values)
theta_ch4 = (7.54, 7.54, 7.54)     # Spherical top
theta_nh3 = (19.9, 19.9, 9.6)      # Symmetric top
theta_h2o = (40.1, 20.9, 13.4)     # Asymmetric top

fig = plt.figure(figsize=(18, 6))

# 1) CH4: Spherical top
ax1 = fig.add_subplot(1, 3, 1, projection='3d')
x1, y1, z1 = surface_points(*theta_ch4)
surf1 = ax1.plot_surface(x1, y1, z1, color='skyblue', alpha=0.4, edgecolor='none')
ax1.set_title("Spherical Top")
ax1.set_box_aspect((1,1,1))
ax1.set_xlim(-7.54, 7.54)
ax1.set_ylim(-7.54, 7.54)
ax1.set_zlim(-7.54, 7.54)
ax1.view_init(elev=20, azim=35)
ax1.set_xlabel('$x$')
ax1.set_ylabel('$y$')
ax1.set_zlabel('$z$')
ax1.set_xticks([])
ax1.set_yticks([])
ax1.set_zticks([])

# Add a CH4 molecule to the plot (schematic coordinates)
positions = np.array([
    [ 0.0000,  0.0000,  0.0000],
    [ 0.6276,  0.6276,  0.6276],
    [ 0.6276, -0.6276, -0.6276],
    [-0.6276,  0.6276, -0.6276],
    [-0.6276, -0.6276,  0.6276]
]) * 7.54/2

for i, pos in enumerate(positions):
    if i == 0:
        ax1.plot(*pos, 'o', markersize=10, markeredgecolor='black', markerfacecolor='black')
    else:
        ax1.plot(*pos, 'o', markersize=5, markeredgecolor='black', markerfacecolor='white')
    if i > 0:
        ax1.plot([positions[0][0], pos[0]],
                 [positions[0][1], pos[1]],
                 [positions[0][2], pos[2]], color='black')

ax1.text(7.54/4, -7.54/4, 7.54/16, 'CH$_4$', color='black', fontsize=12)

# 2) NH3: Symmetric top
ax2 = fig.add_subplot(1, 3, 2, projection='3d')
x2, y2, z2 = surface_points(*theta_nh3)
surf2 = ax2.plot_surface(x2, y2, z2, color='salmon', alpha=0.4, edgecolor='none')
ax2.set_title("Symmetric Top")
ax2.set_box_aspect((1,1,1))
ax2.set_xlim(-19.9, 19.9)
ax2.set_ylim(-19.9, 19.9)
ax2.set_zlim(-19.9, 19.9)
ax2.view_init(elev=20, azim=35)
ax2.set_xlabel('$x$')
ax2.set_ylabel('$y$')
ax2.set_zlabel('$z$')
ax2.set_xticks([])
ax2.set_yticks([])
ax2.set_zticks([])

positions = np.array([
    [ 0.0000,  0.0000,  0.0000],
    [ 0.0000, -0.9377, -0.3816],
    [ 0.8121,  0.4689, -0.3816],
    [-0.8121,  0.4689, -0.3816]
]) * 19.9/2

for i, pos in enumerate(positions):
    if i == 0:
        ax2.plot(*pos, 'o', markersize=10, markeredgecolor='black', markerfacecolor='skyblue')
    else:
        ax2.plot(*pos, 'o', markersize=5, markeredgecolor='black', markerfacecolor='white')
    if i > 0:
        ax2.plot([positions[0][0], pos[0]],
                 [positions[0][1], pos[1]],
                 [positions[0][2], pos[2]], color='black')

ax2.text(19.9/4, -19.9/4, 19.9/16, 'NH$_3$', color='black', fontsize=12)

# 3) H2O: Asymmetric top
ax3 = fig.add_subplot(1, 3, 3, projection='3d')
x3, y3, z3 = surface_points(*theta_h2o)
surf3 = ax3.plot_surface(x3, y3, z3, color='plum', alpha=0.4, edgecolor='none')
ax3.set_title("Asymmetric Top")
ax3.set_box_aspect((1,1,1))
ax3.set_xlim(-40.1, 40.1)
ax3.set_ylim(-40.1, 40.1)
ax3.set_zlim(-40.1, 40.1)
ax3.view_init(elev=20, azim=35)
ax3.set_xlabel('$x$')
ax3.set_ylabel('$y$')
ax3.set_zlabel('$z$')
ax3.set_xticks([])
ax3.set_yticks([])
ax3.set_zticks([])

positions = np.array([
    [ 0.0000,  0.0000,  0.1173],
    [ 0.7572,  0.0000, -0.4692],
    [-0.7572,  0.0000, -0.4692]
]) * 40.1/2

for i, pos in enumerate(positions):
    if i == 0:
        ax3.plot(*pos, 'o', markersize=10, markeredgecolor='black', markerfacecolor='red')
    else:
        ax3.plot(*pos, 'o', markersize=5, markeredgecolor='black', markerfacecolor='white')
    if i > 0:
        ax3.plot([positions[0][0], pos[0]],
                 [positions[0][1], pos[1]],
                 [positions[0][2], pos[2]], color='black')

ax3.text(40.1/4, -40.1/4, 40.1/16, 'H$_2$O', color='black', fontsize=12)

plt.tight_layout()
glue("rotational_symmetry", fig, display=False)
plt.close(fig)

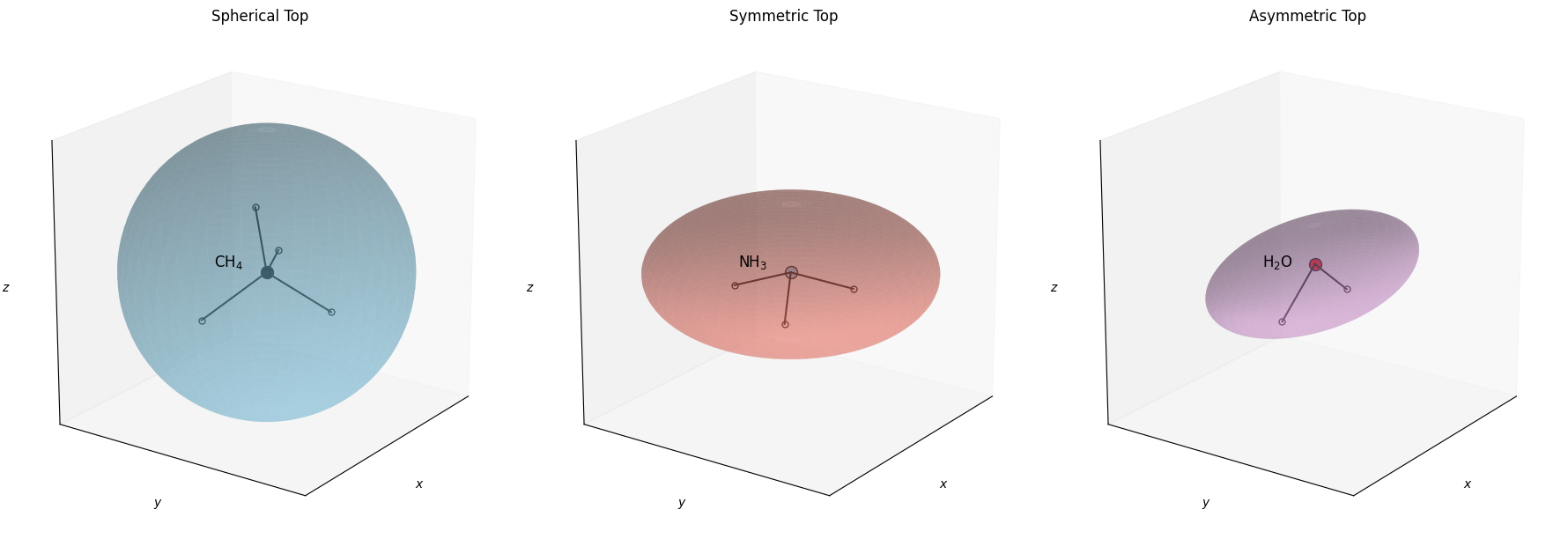
../_images/d9fddeb45593d56215a6dcbfe6ae8ac2627583d5887f7871608d62e6253ba82d.png — Fig. 22 Approximate visualization of rotational shapes for (left) a spherical top (CH₄), (middle) a symmetric top (NH₃), and (right) an asymmetric top (H₂O). The ellipsoids are scaled by \(\sqrt{\Theta_{\text{rot}}}\) in each principal axis direction.#

Vibrations of Polyatomic Molecules#

For a diatomic molecule approximated by a harmonic oscillator of characteristic vibrational temperature \(\Theta_{\text{vib}}\), the vibrational partition function is:

\[q_{\text{vib}} \;=\; \frac{e^{-\Theta_{\text{vib}}/(2T)}}{\,1 - e^{-\Theta_{\text{vib}}/T}\,}.\]

For a polyatomic molecule with \(\alpha\) normal modes (where \(\alpha = 3N - 6\) for a nonlinear molecule and \(\alpha = 3N - 5\) for a linear molecule), the vibrational partition function is the product of each mode’s contribution:

\[q_{\text{vib}} \;=\; \prod_{j=1}^\alpha \; \frac{\,e^{-\Theta_{\text{vib},j}/(2T)}\,}{\,1 - e^{-\Theta_{\text{vib},j}/T}\,}.\]

Here, \(\Theta_{\text{vib},j}\) is the vibrational temperature of the \(j\)-th normal mode.

Electronic Partition Function#

The electronic partition function is given by

\[q_{\text{elec}} \;=\; \sum_{i=1}^{\infty} g_i \, e^{-\beta\,\varepsilon_i} \;\;\underset{\varepsilon_1 = 0}{\longrightarrow}\;\; g_1 \;+\; g_2\,e^{-\beta\,(\varepsilon_2 - \varepsilon_1)} \;+\;\cdots,\]

where \(g_i\) is the degeneracy of the \(i\)-th electronic state, \(\varepsilon_i\) is that state’s electronic energy, and \(\beta = 1/(k_{\text{B}} T)\). In most ground-state-dominated situations (\(\varepsilon_2 - \varepsilon_1 \gg k_{\text{B}} T\)), the higher-lying states contribute negligibly, and \(q_{\text{elec}}\approx g_1\).

Summary#

The table below collects the main partition function formulas for atoms and molecules under typical textbook approximations (high-temperature limit for rotation, harmonic approximation for vibration, negligible excited electronic states):

Table 9 Partition functions for various systems#
System	\(q_{\text{trans}}\)	\(q_{\text{rot}}\)	\(q_{\text{vib}}\)	\(q_{\text{elec}}\)
Atom	\(\frac{V}{\Lambda^3}\)	—	—	\(g_1\)
Diatomic	↓	\(\frac{T}{\sigma\,\Theta_{\text{rot}}}\)	\(\frac{e^{-\Theta_{\text{vib}}/(2T)}}{\,1 - e^{-\Theta_{\text{vib}}/T}\,}\)	↓
Polyatomic	—	—	—	—
Linear	↓	same as diatomic (with adjusted \(\sigma\))	\(\prod_{j=1}^{\alpha}\,\frac{e^{-\Theta_{\text{vib},j}/(2T)}}{1-e^{-\Theta_{\text{vib},j}/T}} \)	↓
Nonlinear	—	—	—	—
Spherical	↓	\(\frac{\sqrt{\pi}}{\sigma}\,\bigl(\tfrac{T}{\Theta_{\text{rot}}}\bigr)^{3/2}\)	↓	↓
Symmetric	↓	\(\frac{\sqrt{\pi}}{\sigma} \sqrt{\frac{T^3}{\Theta_{\text{rot,A}}\,(\Theta_{\text{rot,C}})^2}}\)	↓	↓
Asymmetric	↓	\(\frac{\sqrt{\pi}}{\sigma}\,\sqrt{\frac{T^3}{\Theta_{\text{rot,A}}\,\Theta_{\text{rot,B}}\,\Theta_{\text{rot,C}}}}\)	↓	↓

The translational partition function \(q_{\text{trans}} = \frac{V}{\Lambda^3}\) (with \(\Lambda\) the thermal de Broglie wavelength) applies to all gas-phase systems. For most molecules, the total partition function can be approximated by the product

\[q \;\approx\; q_{\text{trans}}\;q_{\text{rot}}\;q_{\text{vib}}\;q_{\text{elec}},\]

with each factor evaluated using the formulas shown above, assuming the relevant excited states are not significantly populated beyond the ground state.