2.2. Canonical Ensemble

2.2. Canonical Ensemble#

Overview#

In a closed system—one that exchanges energy but not matter with its surroundings—the appropriate statistical description is the canonical ensemble.

../_images/c1023ea376e56e820751f0b23818fdd935f10dad1bb3ffed451b5bef03d0278a.png — Fig. 13 A closed system, exchanging energy but not matter with its surroundings.#

Probability of a Microstate in the Canonical Ensemble#

Consider an ensemble of \(\mathcal{A}\) closed systems exchanging energy with a heat bath at temperature \(T\). A heat bath is an environment that can absorb or release energy without changing its temperature because it is much larger than the system.

How Can an Environment Absorb or Release Energy Without Changing Its Temperature?

The key point is that the temperature of a collection of particles is determined by the average kinetic energy per particle. According to the equipartition theorem, for particles with three translational degrees of freedom the total kinetic energy is

\[E_{\text{kin}} = \frac{3}{2} N\, k_\text{B}\, T.\]

Thus, for a fixed amount of energy transfer, the corresponding change in temperature is given by

\[\Delta T = \frac{2}{3}\frac{\Delta E_\text{kin}}{N\, k_\text{B}}.\]

Because the environment has many more particles than the system (\(N_\text{env} \gg N_\text{sys}\)), the same amount of energy \(\Delta E\) will result in a much smaller \(\Delta T\) for the environment. In our example, even though the system (with \(N_\text{sys} = 6.022\times10^{23}\) particles) absorbs energy and its temperature increases from 300 K to 400 K, the environment (with \(N_\text{env} = 6.022\times10^{24}\) particles, i.e. 10 times as many) loses the same amount of energy per mole but its temperature only drops from 400 K to 390 K.

This illustrates that an environment (or heat bath) can absorb or release energy almost isothermally because its very large number of particles (and hence its high heat capacity) means that the fractional change in average kinetic energy per particle is negligible—even though energy is being exchanged.

Thus, even though the total kinetic energy of the universe (system plus environment) remains constant, the environment’s temperature barely changes because any energy loss or gain is diluted among a huge number of particles.

Ratio of Numbers of Systems in Two Microstates is a Function of Their Relative Energies#

Intuition tells us that a system is more likely to be found in microstates with lower energy.

Building This Intuition

Consider a raindrop that can exist at two different elevations: one high up at Lake Itasca in northern Minnesota and one low down in the Mississippi River in St. Louis. At the higher elevation, the raindrop has more gravitational potential energy, making that state less favorable. Consequently, the raindrop is more likely to be found at the lower elevation, where its gravitational potential energy is reduced. In essence, systems tend to “prefer” lower energy states, which is why, on a macroscopic scale, water naturally flows downhill.

Mathematically, this intuition asserts that the ratio of the numbers \(a_1\) and \(a_2\) of systems in two microstates 1 and 2 is given by

\[\frac{a_2}{a_1} = f \left( E_1, E_2 \right) = f \left( E_1 - E_2 \right),\]

where \(E_1\) and \(E_2\) are the energies of the two microstates. The function \(f\) depends only on the difference in energy between the two states.

Why Does the Ratio Depend Only on the Energy Difference?

The energy of a system is defined relative to an arbitrary (but often convenient) reference level. For example,

The kinetic energy of a moving particle is defined relative to a stationary particle.
The gravitational potential energy of a raindrop is defined relative to the surface of the Earth.

Therefore, the absolute energy of a system is not essential in determining the likelihood of finding the system in a particular microstate, only the difference in energy between two microstates.

Finding an Acceptable Form for \(f\)#

Since \(\{ a_1, a_2, a_3, \ldots \}\) is a set of numbers, we can write

\[\begin{split}\begin{align*} \frac{a_3}{a_1} &= \frac{a_2}{a_1} \times \frac{a_3}{a_2} \\ f \left( E_1 - E_3 \right) &= f \left( E_1 - E_2 \right) \times f \left( E_2 - E_3 \right). \end{align*}\end{split}\]

If \(f\) is “well-behaved” (i.e., continuous, measurable, etc.), it must be of the form

\[f \left( E_m - E_n \right) = e^{\beta \left( E_m - E_n \right)},\]

where \(\beta\) is an undetermined constant, which we will determine later to be \(\frac{1}{k_\text{B} T}\).

Checking the Form of \(f\)

Using this form for \(f\), we can verify that

\[\begin{split}\begin{align*} f \left( E_1 - E_3 \right) &= f \left( E_1 - E_2 \right) \times f \left( E_2 - E_3 \right) \\ e^{\beta \left( E_1 - E_3 \right)} &= e^{\beta \left( E_1 - E_2 \right)} \times e^{\beta \left( E_2 - E_3 \right)} \\ {\color{blue} \cancel{e^{\beta E_1}}} \times {\color{magenta} \cancel{e^{-\beta E_3}}} &= {\color{blue} \cancel{e^{\beta E_1}}} \times {\color{red} \cancel{e^{-\beta E_2}}} \times {\color{red} \cancel{e^{-\beta E_2}}} {\color{magenta} \cancel{e^{-\beta E_3}}} \\ 1 &= 1. \end{align*}\end{split}\]

Converting \(f\) to a Probability#

Separating the variables with indices \(m\) and \(n\),

\[a_m e^{\beta E_m} = a_n e^{\beta E_n} = \mathcal{C},\]

where \(\mathcal{C}\) is a constant. Therefore, the number of systems in a microstate with energy \(E_m\) is

\[a_m = \mathcal{C} e^{-\beta E_m}.\]

The constant \(\mathcal{C}\) is determined by the normalization condition

\[\sum_m a_m = \mathcal{A} = \mathcal{C} \sum_m e^{-\beta E_m},\]

Solving the second equation for \(\mathcal{C}\) and substituting it into the equation for \(a_m\) gives

(13)#\[p_m = \frac{a_m}{\mathcal{A}} = \frac{e^{-\beta E_m}}{\sum_m e^{-\beta E_m}} = \frac{e^{-\beta E_m}}{Q},\]

where \(p_m\) is the probability of finding the system in microstate \(m\) and \(Q\) is called the partition function, which is the essential quantity in statistical mechanics.

Two-State System#

Consider a system with two states: state 1 with energy \(E_1\) and state 2 with energy \(E_2\).

Table 7 Chemical Contexts Where a Two-State Approximation Might be Appropriate#
Chemical Context	State 1	State 2
Electronic transitions in atoms or molecules	Ground state	Excited state
Donor–acceptor electron transfer	Reduced state	Oxidized state
Molecular isomerization	Reactant	Product
Defects in solids	Defect-free	Defective
Protein folding	Unfolded	Folded

Partition Function for a Two-State System#

The partition function \(Q_\text{two-state}\) for a two-state system is

\[\begin{split}\begin{align*} Q_\text{two-state} &= e^{-\beta E_1} + e^{-\beta E_2} \\ &= e^{-\beta E_1} \left( 1 + e^{-\beta \Delta E} \right), \end{align*}\end{split}\]

where \(\Delta E = E_2 - E_1\) is the energy difference between the two states.

Probability of Finding the System in State 1#

The probability of finding the system in state 1 is

\[p_1 = \frac{e^{-\beta E_1}}{Q_\text{two-state}} = \frac{1}{1 + e^{-\beta \Delta E}} = \frac{1}{1 + e^{-\frac{\Delta E}{k_\text{B} T}}}.\]

Probability of Finding the System in State 2#

The probability of finding the system in state 2 is

\[p_2 = 1 - p_1\]

Partition Function as the Effective Number of Thermally Accessible Microstates#

Show code cell source Hide code cell source

import numpy as np
import matplotlib.pyplot as plt
from scipy.constants import k, eV
from labellines import labelLines
from myst_nb import glue
from matplotlib.patches import Rectangle

k_B = k / eV  # Boltzmann constant in eV/K

# Define the partition function for a two-state system
def partition_function_two_state(E1, E2, T):
    beta = 1 / (k_B * T)
    return np.exp(-beta * E1) + np.exp(-beta * E2)

# Calculate the partition function for a two-state system
E1 = 0
E2 = 0.01  # Energy difference between the two states in eV
T_values = np.linspace(1, 1000, 1000)
Q_values = [partition_function_two_state(E1, E2, T) for T in T_values]

# Calculate the probabilities of finding the system in each state for a two-state system
p1_values = [np.exp(-1 / (k_B * T) * E1) / Q for T, Q in zip(T_values, Q_values)]
p2_values = [np.exp(-1 / (k_B * T) * E2) / Q for T, Q in zip(T_values, Q_values)]

# Plot the partition function and the probabilities of finding the system in each state
fig, axs = plt.subplots(1, 2, figsize=(8, 4))

# Plot the partition function on axs[0]
axs[0].plot(T_values, Q_values, 'k-')
axs[0].set_xlabel('Temperature (K)')
axs[0].set_ylabel('$Q_{\\text{two-state}}$')
axs[0].grid(True)
axs[0].annotate(
    '$\\rightarrow 1$ accessible\nmicrostate', xy=(40, Q_values[0] + 0.01), xytext=(300, 1.1),
    arrowprops=dict(arrowstyle='->', color='b'),
    bbox=dict(boxstyle='round,pad=0.3', fc='w', ec='b'),
    ha='center', va='center', color='b'
)
axs[0].annotate(
    '$\\rightarrow 2$ accessible\nmicrostates', xy=(T_values[-1], Q_values[-1]), xytext=(750, 1.7),
    arrowprops=dict(arrowstyle='->', color='m'),
    bbox=dict(boxstyle='round,pad=0.3', fc='w', ec='m'),
    ha='center', va='center', color='m'
)
axs[0].set_xlim(0, 1000)
axs[0].set_ylim(1, 2)

# Plot the probabilities of finding the system in each state on axs[1]
p1_line, = axs[1].plot(T_values, p1_values, 'b-', label='State 1')
p2_line, = axs[1].plot(T_values, p2_values, 'r-', label='State 2')
labelLines([p1_line, p2_line], zorder=2.5)
axs[1].set_xlabel('Temperature (K)')
axs[1].set_ylabel('Probability')
axs[1].grid(True)
axs[1].set_ylim(0, 1)  # ensure y-axis spans from 0 to 1

# Add tall outlined rectangles around the probabilities at low and high temperatures.
# For T -> 0: highlight T from 1 to 50 K.
# For T = 1000: highlight T from 950 to 1000 K.
rect_low = Rectangle((1, 0), 50 - 1, 1, edgecolor='b', facecolor='b', linestyle='-', alpha=0.2)
rect_high = Rectangle((950, 0), 1000 - 950, 1, edgecolor='m', facecolor='m', linestyle='-', alpha=0.2)
axs[1].add_patch(rect_low)
axs[1].add_patch(rect_high)
axs[1].annotate(
    'Only state 1 is accessed', xy=(50, 0.95), xytext=(100, 0.95),
    arrowprops=dict(arrowstyle='-', color='b'),
    ha='left', va='center', color='b'
)
axs[1].annotate(
    'Both states are accessed', xy=(950, 0.05), xytext=(900, 0.05),
    arrowprops=dict(arrowstyle='-', color='m'),
    ha='right', va='center', color='m'
)

plt.tight_layout()
glue('two-state-system', fig, display=False)
plt.close(fig)

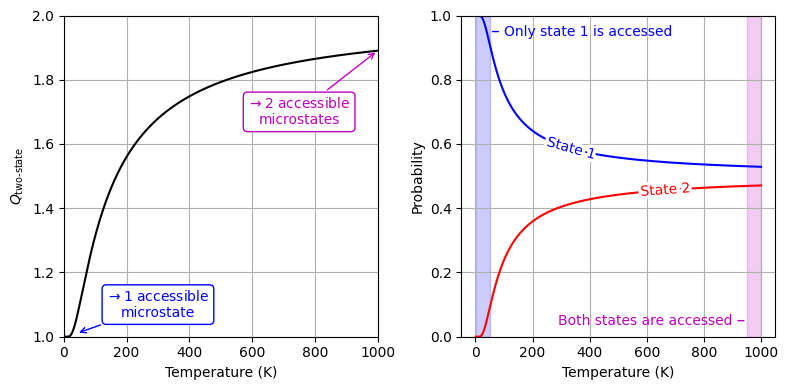
../_images/1cb5dbb14bb2d63e860d0aa471f68ff97184bc7c8ea02c47f8e6497410268298.png — Fig. 14 Partition function of a two-state system and the probabilities of finding it in each state as a function of temperature. The energy difference between the two states is 0.01 eV.#