2.6. Harmonic Oscillator

2.6. Harmonic Oscillator#

Overview#

This section discusses the quantum mechanical treatment of a harmonic oscillator, along with the derivation of key thermodynamic properties using the partition function. We begin with a review of the one-dimensional case, generalize to three dimensions, and then show how the classical partition function emerges in the high-temperature limit.

Review of the One-Dimensional Harmonic Oscillator#

Show code cell source Hide code cell source

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d.art3d import Poly3DCollection
from scipy.constants import k, eV
from scipy.special import hermite, factorial
from labellines import labelLines
from myst_nb import glue
from numpy.linalg import eigh

fig, axs = plt.subplot_mosaic([[0]], figsize=(4, 4))

def harmonic_potential(x, m, omega):
    """
    Calculates the potential matrix for a particle in a one-dimensional harmonic potential
    
    Parameters
    ----------
    x : array-like
        The positions of the particles.
    m : float
        The mass of the particle.
    omega : float
        The frequency of the harmonic potential
    
    Returns
    -------
    array
        The potential matrix.
    """
    V = 0.5 * m * omega**2 * x**2
    V_matrix = np.diag(V)
    return V_matrix

def off_diagonal_identity_matrix(n_points):
    matrix = np.zeros((n_points, n_points))
    for i in range(n_points):
        if i == 0:
            matrix[i + 1, i] = 1
        elif i == n_points - 1:
            matrix[i - 1, i] = 1
        else:
            matrix[i - 1, i] = 1
            matrix[i + 1, i] = 1
    return matrix

def laplacian_matrix(x):
    """
    Calculates the Laplacian matrix for a particle in a one-dimensional potential.
    
    Parameters
    ----------
    x : array-like
        The positions of the particles.
    
    Returns
    -------
    array
        The Laplacian matrix.
    """
    Delta_x = x[1] - x[0]
    n_points = len(x)
    off_diag = off_diagonal_identity_matrix(n_points)
    Laplacian = (1 / (Delta_x**2)) * (-2 * np.eye(n_points) + off_diag)
    return Laplacian

# Define constants in atomic units
hbar = 1
m = 1

# Harmonic potential
omega = 1

# Discretize the system
n_points = 2000
L = 40
x = np.linspace(-L/2, L/2, n_points)

# Construct the Hamiltonian matrix
H_harm = -hbar**2 / (2 * m) * laplacian_matrix(x) + harmonic_potential(x, m=1, omega=1)

# Solve for eigenvalues and eigenfunctions
E_harm, psi_harm = np.linalg.eigh(H_harm)

# Plot a one-dimensional quadratic potential
axs[0].plot(x, np.diag(harmonic_potential(x, m, omega)), "k-", zorder=2.5, lw=4)

# Plot the energy levels (blue lines)
for n in range(4):
    energy = axs[0].plot(x, np.ones_like(x) * E_harm[n], color='blue', label=r'$E_{%d}$' % n)
    labelLines(energy, xvals=[-L/24], zorder=2.5)

# Plot the wavefunctions (red curves)
for n in range(4):
    wavefunction = axs[0].plot(x, psi_harm[:, n] * 4 + E_harm[n], color='red', label=r'$\psi_{%d}$' % n)
    labelLines(wavefunction, xvals=[L/24], zorder=2.5)

# Format plot
axs[0].set_xlim(-L/8, L/8)
ymin = np.min(np.diag(harmonic_potential(x, m, omega)))
ymax = np.max(psi_harm[:, -1]) + E_harm[3]
yrange = ymax - ymin
ybuffer = 0.05 * yrange
axs[0].set_ylim(ymin - ybuffer, ymax + ybuffer * 2)
axs[0].set_xlabel("Position")
axs[0].set_ylabel("Energy")
axs[0].set_xticks([])
axs[0].set_yticks([])
axs[0].spines['top'].set_visible(False)
axs[0].spines['right'].set_visible(False)
axs[0].spines['left'].set_visible(False)
axs[0].spines['bottom'].set_visible(False)

plt.tight_layout()
glue("harmonic_oscillator", fig, display=False)
plt.close(fig)

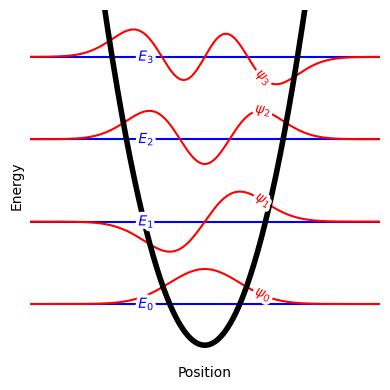
../_images/9bb5b52df8d59477dab5ccc5dd84aa926cec2bc961cc27ffb6b07499c897b099.png — Fig. 17 Enery levels and wavefunctions for a one-dimensional harmonic oscillator. The energy levels \(E_n\) are shown as blue lines, while the wavefunctions \(\psi_n\) are shown as red curves.#

For a one-dimensional harmonic oscillator of frequency \(\omega\), the quantized energy levels are given by

\[E_n = \hbar \omega \left( n + \frac{1}{2} \right) \quad \text{for} \; n = 0, 1, 2, \ldots,\]

where \(\hbar\) is the reduced Planck constant and \(n\) is a positive integer.

Partition Function for a Harmonic Oscillator#

The partition function for a one-dimensional harmonic oscillator is:

\[\begin{split}\begin{aligned} q &= \sum_{n=0}^{\infty} e^{-\beta E_n} \\ &= \sum_{n=0}^{\infty} e^{-\beta \hbar \omega (n + 1/2)} \\ &= e^{-\beta \hbar \omega / 2} \sum_{n=0}^{\infty} e^{-\beta \hbar \omega n} \\ \end{aligned}\end{split}\]

Evaluation of the Sum#

The \(\sum_{n=0}^{\infty} e^{-\beta \hbar \omega n}\) term is a geometric series, which can be evaluated as

\[\sum_{n=0}^{\infty} x^n = \frac{1}{1 - x} \quad \text{for} \; |x| < 1.\]

Substituting \(x = e^{-\beta \hbar \omega}\) gives:

\[q = \frac{e^{-\beta \hbar \omega / 2}}{1 - e^{-\beta \hbar \omega}}.\]

Is \(|x| < 1\)?

\[\begin{split}\begin{aligned} |x| &< 1 \\ \left| e^{-\beta \hbar \omega} \right| &< 1 \\ e^{-\beta \hbar \omega} &< 1 \\ \beta \hbar \omega &> 0 \\ \beta &> 0. \end{aligned}\end{split}\]

Ensemble Averages for a Harmonic Oscillator#

Natural Logarithm of the Partition Function#

Taking the logarithm of \(q\):

(21)#\[\ln q = -\frac{\beta \hbar \omega}{2} - \ln(1 - e^{-\beta \hbar \omega}).\]

Internal Energy#

The internal energy \(U\) is found via:

\[U = -\left( \frac{\partial \ln q}{\partial \beta} \right)_{N, V} = \frac{\hbar \omega}{2} + \frac{\hbar \omega}{e^{\beta \hbar \omega} - 1}.\]

Derivative of \(\ln(1 - e^{-\beta \hbar \omega})\)

\[\begin{split}\begin{aligned} \left[ \frac{\partial}{\partial \beta} \ln(1 - e^{-\beta \hbar \omega}) \right]_{N, V} &= \left[ \frac{\partial \ln f}{\partial f} \frac{\partial f}{\partial \beta} \right]_{N, V} && \text{where} \; f = 1 - e^{-\beta \hbar \omega} \\ &= \frac{1}{f} \left[ \frac{\partial}{\partial \beta} (1 - e^{-\beta \hbar \omega}) \right]_{N, V} \\ &= \frac{\hbar \omega e^{-\beta \hbar \omega}}{1 - e^{-\beta \hbar \omega}} \cdot \frac{e^{\beta \hbar \omega}}{e^{\beta \hbar \omega}} \\ &= \frac{\hbar \omega}{e^{\beta \hbar \omega} - 1}. \end{aligned}\end{split}\]

We often define the vibrational temperature \(\Theta_{\text{vib}}\) as

\[\Theta_{\text{vib}} = \frac{\hbar \omega}{k_{\text{B}}}.\]

Hence,

\[U = \frac{\hbar \omega}{2} + \frac{\hbar \omega}{e^{\Theta_{\text{vib}} / T} - 1}.\]

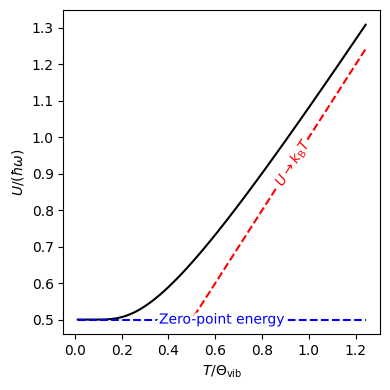
../_images/54639f431ca0624b6f6131fac8c83dfe72866c8aba3dd08f74b25687f4a533ee.png — Fig. 18 Internal energy of a harmonic oscillator as a function of temperature. The zero-point energy is shown as a blue dashed line, while the high-temperature limit is shown as a red dashed line.#

Heat Capacity at Constant Volume#

In Section 2.3, we showed that

\[\sigma_E^2 = \left( \frac{\partial^2 \ln q}{\partial \beta^2} \right)_{N, V} = k_{\text{B}} T^2 C_V.\]

From Equation (21), it follows that:

\[C_V = k_{\text{B}} \left( \frac{\hbar \omega}{k_{\text{B}} T} \right)^2 \frac{e^{\hbar \omega / k_{\text{B}} T}}{\left( e^{\hbar \omega / k_{\text{B}} T} - 1 \right)^2} = k_{\text{B}} \left( \frac{\Theta_{\text{vib}}}{T} \right)^2 \frac{e^{\Theta_{\text{vib}} / T}}{\left( e^{\Theta_{\text{vib}} / T} - 1 \right)^2}.\]

Complete Derivation of \(C_V\)

\[\begin{split}\begin{aligned} \sigma_E^2 &= \left[ \frac{\partial^2}{\partial \beta^2} \left( -\frac{\beta \hbar \omega}{2} - \ln(1 - e^{-\beta \hbar \omega}) \right) \right]_{N, V} \\ &= \left[ \frac{\partial}{\partial \beta} \left( -\frac{\hbar \omega}{2} - \frac{\hbar \omega}{e^{\beta \hbar \omega} - 1} \right) \right]_{N, V} \\ &= -\hbar \omega \left( \frac{\partial g^{-1}}{\partial g} \frac{\partial g}{\partial \beta} \right)_{N, V} && \text{where} \; g = e^{\beta \hbar \omega} - 1 \\ &= \frac{\hbar \omega}{g^2} \left[ \frac{\partial}{\partial \beta} \left( e^{\beta \hbar \omega} - 1 \right) \right]_{N, V} \\ &= \left( \hbar \omega \right)^2 \frac{e^{\beta \hbar \omega}}{\left( e^{\beta \hbar \omega} - 1 \right)^2} \\ \end{aligned}\end{split}\]

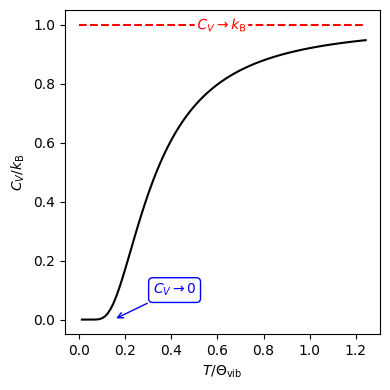
../_images/d91ac4ae095085f8fa74f058239922e1778dc5520c7ff5d3d2b9fbc797f6cf44.png — Fig. 19 Heat capacity at constant volume of a harmonic oscillator as a function of temperature. The low-temperature limit is shown as a blue arrow, while the high-temperature limit is shown as a red dashed line.#

Einstein Model#

The Einstein model is a simple model for an atomic crystal, where \(N\) identical atoms are situated at lattice sites and vibrate (each with the same frequency) about these sites as independent (i.e., non-interacting), three-dimensional harmonic oscillators. Since the atoms are situated at lattice sites, they can be treated as distinguishable. For the Einstein model, the partition function is

\[Q = q^{3N} = \left( \frac{e^{-\beta \hbar \omega / 2}}{1 - e^{-\beta \hbar \omega}} \right)^{3N}.\]

One can show that

\[U = \frac{3}{2} N \hbar \omega + \frac{3N \hbar \omega}{e^{\beta \hbar \omega} - 1},\]

and

\[C_V = 3 N k_{\text{B}} \left( \frac{\hbar \omega}{k_{\text{B}} T} \right)^2 \frac{e^{\hbar \omega / k_{\text{B}} T}}{\left( e^{\hbar \omega / k_{\text{B}} T} - 1 \right)^2}.\]

Dulong-Petit Law#

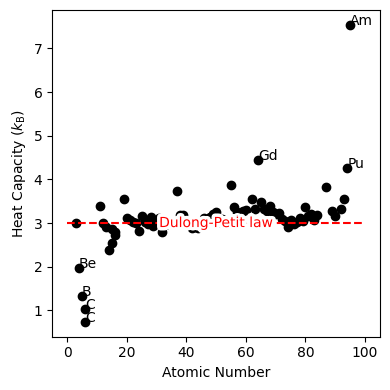
../_images/639220a712e025552e3c458a7d5fd6735c9083d89b0838b030e13cea404b78da.png — Fig. 20 Heat capacity of elemental solids as a function of atomic number. The Dulong-Petit law is shown as a red dashed line.#