2.3. Ensemble Averages#
Overview#
In Section 2.1, we introduced the concept that macroscopic properties are expected values of microscopic properties, emphasizing that these expected values account for the probabilities of different microstates. In Section 2.2, we derived the probability distribution (in the canonical ensemble) for a closed system’s microstates. Now, in this section, we connect these ideas to calculate ensemble averages that determine macroscopic properties.
Thermodynamic Equilibrium#
Recall from Section 1.1 that thermodynamic equilibrium is a state of simultaneous mechanical, thermal, and chemical equilibrium. Below are definitions of each type of equilibrium:
- Thermal contact#
A state in which two systems can exchange energy.
- Chemical contact#
A state in which two systems can exchange matter.
- Mechanical equilibrium#
A state where the net force on every particle in the system is zero.
- Thermal equilibrium#
A state where there is no net exchange of energy between systems in thermal contact.
- Chemical equilibrium#
A state where there is no net exchange of matter between systems in chemical contact.
Internal Energy#
The internal energy \(U\) of a macroscopic system at thermodynamic equilibrium is defined as the ensemble average \(\langle E \rangle\) of the total microscopic energy \(E\):
where \(E_i\) is the energy of microstate \(i\), \(p_i\) is the probability of that microstate, and \(M\) is the total number of microstates.
For the canonical ensemble, using the Boltzmann factor and the partition function \(Q\), we have
where \(\beta = 1/(k_{\text{B}} T)\) and
Why can we factor out \(Q\)?
Since \(Q\) is defined at fixed \(N, V,\) and \(T\), it does not depend on the microstate index \(i\). Consequently, \(Q\) behaves as a constant with respect to the summation over \(i\).
Partial Derivative of the Partition Function#
Taking the partial derivative of \(Q\) with respect to \(\beta\) yields:
Substitute into the expression for \(U\):
Where does the natural log come in?
Using the chain rule,
Example: Two-State System#
For a two-state system with energies \(E_1\) and \(E_2\), the partition function is
Then the internal energy is
which is the ensemble average \(\langle E\rangle\).
Consistency Check
Since \(Q_{\text{two-state}} = e^{-\beta E_1} + e^{-\beta E_2}\), we see
Show code cell source
import numpy as np
import matplotlib.pyplot as plt
from scipy.constants import k, eV
from scipy.differentiate import derivative
from labellines import labelLines
from myst_nb import glue
from matplotlib.patches import Rectangle
kB = k / eV # Boltzmann constant in eV/K
# Define the partition function for a two-state system
def partition_function_two_state(E1, E2, T):
beta = 1 / (kB * T)
return np.exp(-beta * E1) + np.exp(-beta * E2)
# Calculate the partition function for a two-state system
E1 = 0
E2 = 0.01 # Energy difference between the two states in eV
T_values = np.linspace(1, 1000, 1000)
Q_values = [partition_function_two_state(E1, E2, T) for T in T_values]
# Calculate the internal energy for a two-state system
beta_values = 1 / (kB * T_values)
ln_Q_values = np.log(Q_values)
U_values = -np.gradient(ln_Q_values, beta_values)
# Plot the internal energy as a function of temperature
fig, ax = plt.subplots(figsize=(4, 4))
ax.plot(T_values, U_values, 'k-')
ax.set_xlabel('Temperature (K)')
ax.set_ylabel('$U_{\\text{two-state}} - E_1$ (eV)')
ax.grid(True)
ax.annotate(
'$U_{\\text{two-state}} \\rightarrow E_1$', xy=(40, U_values[0] + 0.0001), xytext=(300, 0.001),
arrowprops=dict(arrowstyle='->', color='b'),
bbox=dict(boxstyle='round,pad=0.3', fc='w', ec='b'),
ha='center', va='center', color='b'
)
x_values_high_T = np.linspace(0, 1000, 1001)
y_values_high_T = ((E1 + E2) / 2) * np.ones_like(x_values_high_T)
line = ax.plot(x_values_high_T, y_values_high_T, 'm--', label='$U_{\\text{two-state}} \\rightarrow (E_1 + E_2) / 2$')
labelLines(line, zorder=2.5)
ax.set_xlim(0, 1000)
ax.set_ylim(0, 0.01)
plt.tight_layout()
glue("fig:ensemble-average-internal-energy-two-state", fig, display=False)
plt.close(fig)
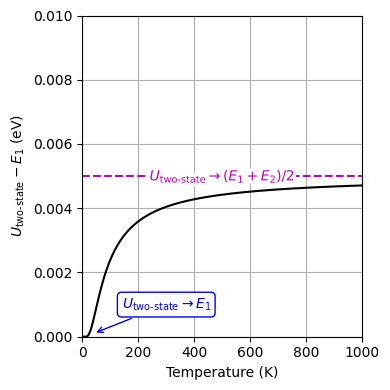
Fig. 15 Internal energy of a two-state system as a function of temperature. The energy difference between the two states is 0.01 eV.#
Heat Capacity at Constant Volume#
From Section 1.1, heat is energy transferred due to a temperature difference. The heat capacity at constant volume, \(C_V\), measures how much heat is required to change a system’s temperature at fixed \(N\) and \(V\):
Heat Capacity and Energy Fluctuations#
In statistics, the variance \(\sigma_X^2\) of a random variable \(X\) is \(\sigma_X^2 = \langle (X - \langle X\rangle)^2\rangle\). In statistical mechanics, \(\sigma_E^2\) represents fluctuations in total energy:
One can show that
which implies
What does the relationship mean physically?
A larger heat capacity corresponds to bigger energy fluctuations, indicating the system readily absorbs or releases energy. Conversely, smaller energy fluctuations suggest the system is less prone to exchanging energy with its surroundings.
Complete Derivation of the \(C_V\) and \(\sigma_E^2\) Relationship
1. Demonstrate that \(\left( \partial^2 \ln Q / \partial \beta^2 \right)_{N, V} = \sigma_E^2\)
2. Establish that \(\left( \partial T / \partial \beta \right)_{N, V} = -k_{\text{B}} T^2\)
3. Prove that \(\left( \partial^2 \ln Q / \partial \beta^2 \right)_{N, V} = k_{\text{B}} T^2 C_V\)
4. Set Results from Step 1 and 3 Equal to Each Other and Solve for \(C_V\)
Pressure#
In Module 5, we will derive:
\(A = -k_{\text{B}}\,T\ln Q\), where \(A\) is the Helmholtz free energy.
\(P = -\left(\frac{\partial A}{\partial V}\right)_{N,T}\), where \(P\) is pressure.
Combining these, we find
