1.2. Kinetic Theory

1.2. Kinetic Theory#

Overview#

Kinetic theory connects the microscopic motion of gas particles to macroscopic properties such as pressure and temperature. This section introduces the fundamental assumptions of kinetic theory, derives key equations, and highlights their physical relevance.

Foundational Assumptions of Kinetic Theory#

  1. Large Number of Particles: A gas contains a very large number of identical particles moving randomly in all directions.

  2. Point Particles: Each particle’s size is negligible compared to the average distance between particles.

  3. Elastic Collisions: Collisions between particles, and between particles and the container walls, conserve both momentum and kinetic energy.

  4. No Long-Range Interparticle Forces: Particles do not exert forces on one another except when they collide (i.e., there are no long-range attractive or repulsive forces).

  5. Classical Mechanics Applies: Particle motion follows Newton’s second law:

    \[\vec{F} = \frac{d\vec{p}}{dt},\]

    where \(\vec{F}\) is the net force on a particle, \(\vec{p}\) is its linear momentum, and \(t\) is time.

Deriving Pressure from Particle-Wall Collisions#

Hide code cell source 
import matplotlib.pyplot as plt
from myst_nb import glue

def plot_container_2d(offset=0.2):
    """Plot a 2D schematic of a gas particle in a container."""
    fig, ax = plt.subplots(figsize=(12, 4))

    # Dimensions
    Lx, Lz = 10, 2

    # Draw container
    ax.plot([0, Lx, Lx, 0, 0], [0, 0, Lz, Lz, 0], color='black')
    ax.fill_between([0, Lx], 0, Lz, color='lightgray')

    # Gas particle
    ax.plot(0.5 * Lx, 0.75 * Lz, 'o', color='blue', markersize=20, zorder=10)
    ax.text(0.5 * Lx, 0.75 * Lz, "$m$", color='white',
            ha='center', va='center', zorder=20, fontsize=12)

    # Velocity arrows
    ax.annotate("", xy=(0.5 * Lx, 0.75 * Lz), xytext=(Lx, 0.75 * Lz),
                arrowprops=dict(arrowstyle="<-", color='red'))
    ax.text(Lx * 2 / 3, 0.75 * Lz + offset, "$v_x$", color='red', fontsize=12, ha='center', va='center')

    ax.annotate("", xy=(Lx, 0.5 * Lz), xytext=(0, 0.5 * Lz),
                arrowprops=dict(arrowstyle="<-", color='red'))
    ax.text(Lx * 5 / 6, 0.5 * Lz + offset, "$-v_x$", color='red', fontsize=12, ha='center', va='center')

    ax.annotate("", xy=(0, 0.25 * Lz), xytext=(0.5 * Lx, 0.25 * Lz),
                arrowprops=dict(arrowstyle="<-", color='red'))
    ax.text(0.25 * Lx, 0.25 * Lz + offset, "$v_z$", color='red', fontsize=12, ha='center', va='center')

    # Length indicators
    ax.annotate("", xy=(0, -offset), xytext=(Lx, -offset),
                arrowprops=dict(arrowstyle="<->", color='black'))
    ax.text(Lx / 2, -2 * offset, "$L_x$", color='black', fontsize=12, ha='center', va='center')

    ax.annotate("", xy=(-offset, 0), xytext=(-offset, Lz),
                arrowprops=dict(arrowstyle="<->", color='black'))
    ax.text(-2 * offset, Lz / 2, "$L_z$", color='black', fontsize=12, ha='center', va='center')

    ax.set_xlim(-1, Lx+1)
    ax.set_ylim(-1, Lz+1)
    ax.axis('off')

    return fig

fig = plot_container_2d()
glue('gas-in-container', fig, display=False)
plt.close(fig)
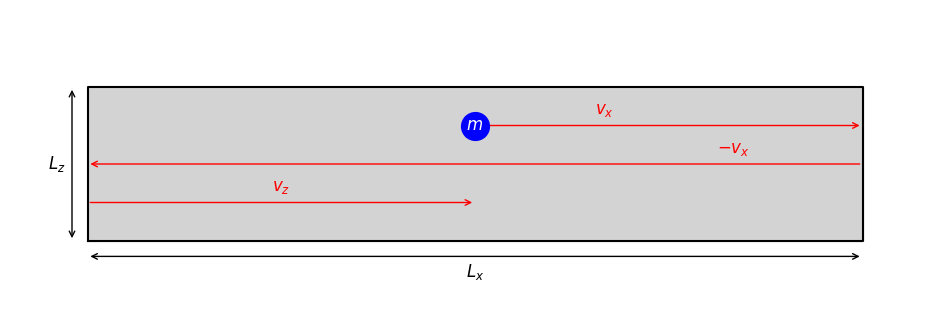
../_images/e02e7de3d45af02cee190256cc5d1497021366c4e768a9b744b9178c9935b014.png

Fig. 5 A two-dimensional representation of a single gas particle in a cuboid container (gray). Velocity components are shown in red. The length \(L_y\) is not depicted, as it extends perpendicular to the plane of view.#

Microscopic Picture of Pressure#

Pressure is the force exerted per unit area on the container walls. On a microscopic level, this force comes from the collective effect of countless collisions of gas particles with the walls.

Particle Momentum Change#

For an elastic collision of a particle of mass \(m\) moving with velocity \(v_x\) in the \(x\)-direction, the momentum change is:

\[\Delta p_x = 2 m v_x.\]

Time Between Collisions#

If the container has length \(L_x\) in the \(x\)-direction, the time between two consecutive collisions of the same particle with that wall is:

\[\Delta t = \frac{2 L_x}{v_x}.\]

Force on the Wall#

A single particle’s average force on the wall (in the \(x\)-direction) is then:

\[F_{\text{p}, x} = \frac{\Delta p_x}{\Delta t} = \frac{m v_x^2}{L_x}.\]

Total Pressure#

For \(N\) identical particles with isotropic motion in a volume \(V\), the total pressure \(P\) is:

\[P = \frac{1}{V} \sum_{i=1}^N \frac{1}{3} m v_i^2,\]

where \(v_i\) is the speed of the \(i\)-th particle. Using the average speed squared \(\langle v^2 \rangle\), we get:

(1)#\[P = \frac{N m \langle v^2 \rangle}{3 V}.\]

This equation shows how the macroscopic pressure depends on the microscopic speeds of the particles.

Kinetic Energy and Temperature#

The average translational kinetic energy per particle is:

\[\langle E_\text{kin} \rangle = \frac{1}{2} m \langle v^2 \rangle.\]

From the ideal gas equation of state \(P V = N k_\text{B} T\) (to be discussed in Section 3), one can show that

(2)#\[\frac{1}{2} m \langle v^2 \rangle = \frac{3}{2} k_\text{B} T,\]

where \(k_\text{B}\) is the Boltzmann constant and \(T\) is the absolute temperature. This result—called the equipartition theorem—indicates that the temperature is directly proportional to the average kinetic energy of the particles.

Complete Derivation of the Relationship Between Kinetic Energy and Temperature

1. Kinetic Energy of a Single Particle: Consider a single particle with mass \(m\) and velocity \(v\). Its translational kinetic energy is given by

\[E_{\text{p},\,\text{kin}} \;=\; \frac{1}{2}\,m\,v^{2}.\]

2. Total Kinetic Energy of \(N\) Particles: For \(N\) particles with masses \(m_1, m_2, \ldots, m_N\) and respective velocities \(v_1, v_2, \ldots, v_N\), the total translational kinetic energy is

\[E_{\text{kin}}\left(m_1,\ldots,m_N\right) \;=\; \frac{1}{2}\,\sum_{i=1}^{N} m_i\,v_i^2.\]

If all particles are identical with mass \(m\), the total kinetic energy simplifies to

\[E_{\text{kin}} \;=\; \frac{1}{2}\,m\,\sum_{i=1}^{N} v_i^2.\]

3. Defining the Average of the Velocity Squared: We define the average of the velocity squared as

\[\langle v^2 \rangle \;=\; \frac{1}{N}\,\sum_{i=1}^{N} v_i^2,\]

so that

\[\sum_{i=1}^{N} v_i^2 \;=\; N\,\langle v^2 \rangle.\]

Substituting this back into the expression for the total kinetic energy of \(N\) identical particles gives

Total Kinetic Energy of \(N\) Identical Particles

\[E_{\text{kin}} \;=\; \frac{1}{2}\,N\,m\,\langle v^2 \rangle.\]

4. Relating Pressure to Kinetic Energy: From Equation (1), the pressure \(P\) in a volume \(V\) can be written as

\[P \;=\; \frac{N\,m\,\langle v^2 \rangle}{3\,V}.\]

Recognizing that \(N m \langle v^2 \rangle / 2 = E_{\text{kin}}\), we see:

\[P \;=\; \frac{2\,E_{\text{kin}}}{3\,V}.\]

5. Equating to the Ideal Gas Equation of State: According to the ideal gas equation of state (to be discussed in Section 3), the pressure is also given by

\[P \;=\; \frac{N\,k_\text{B}\,T}{V},\]

where \(k_\text{B}\) is the Boltzmann constant and \(T\) is the absolute temperature. Equating the two expressions for pressure,

\[\frac{2\,E_{\text{kin}}}{3\,V} \;=\; \frac{N\,k_\text{B}\,T}{V}.\]

Solving for \(E_{\text{kin}}\):

\[E_{\text{kin}} \;=\; \frac{3}{2}\,N\,k_\text{B}\,T.\]

6. Average Kinetic Energy Per Particle (Equipartition Theorem): Dividing both sides by \(N\), we obtain the average kinetic energy of a single particle:

Important

\[\langle E_{\text{kin}} \rangle \;=\; \frac{E_{\text{kin}}}{N} \;=\; \frac{1}{2}\,m\,\langle v^2 \rangle \;=\; \frac{3}{2}\,k_\text{B}\,T.\]

Each translational degree of freedom contributes \(k_\text{B} T / 2\) to the average kinetic energy.

Estimating Particle Speeds#

By rearranging Equation (2), we obtain the root-mean-square (rms) speed:

(3)#\[v_{\text{rms}} = \sqrt{\frac{3 k_\text{B} T}{m}}.\]

This expression shows that:

  • Hotter gases (larger \(T\)) have faster particles.

  • For a given temperature, lighter particles (smaller \(m\)) move faster than heavier ones.

Example: Speed of Air Molecules at Room Temperature

Air is roughly 78% nitrogen (N\(_2\)) by volume. Thus, a good estimate for the speed of air molecules at around 300 K is the rms speed of an N\(_2\) molecule at 300 K.

Using the molar mass of N\(_2\), \(M_\text{r} = 28.0134\,\text{g/mol}\),[1] one finds:

\[v_{\text{rms}} = \sqrt{\frac{3 k_\text{B} T}{M_\text{r} / N_\text{A}}} \approx 517\,\text{m/s} \approx 1{,}156\,\text{mph}.\]

This speed is significantly faster than a Boeing 747-8 airliner at cruising velocity (about 660 mph).[2]