Appendix B. Thermal Energy#
Show code cell source
import numpy as np
import matplotlib.pyplot as plt
from labellines import labelLines
from myst_nb import glue
from scipy.constants import k, eV
def find_turning_points(x, potential, energy):
"""
Find the left and right classical turning points for a given energy level.
Parameters:
x (np.ndarray): Array of distances.
potential (np.ndarray): Potential energy values corresponding to x.
energy (float): The energy level for which to find the turning points.
Returns:
tuple: (x_left, x_right) where each is the interpolated turning point.
Returns (None, None) if fewer than two intersections are found.
"""
diff = potential - energy
indices = np.where(np.diff(np.sign(diff)))[0]
if len(indices) < 2:
return None, None
i_left, i_right = indices[0], indices[-1]
x_left = x[i_left] - diff[i_left] * (x[i_left+1] - x[i_left]) / (diff[i_left+1] - diff[i_left])
x_right = x[i_right] - diff[i_right] * (x[i_right+1] - x[i_right]) / (diff[i_right+1] - diff[i_right])
return x_left, x_right
def morse_potential(x, D_e, a, r_e, offset=0):
"""
Compute the Morse potential.
Parameters:
x (np.ndarray): Array of distances.
D_e (float): Depth of the potential.
a (float): Width parameter.
r_e (float): Equilibrium distance.
offset (float): Energy offset (default is 0).
Returns:
np.ndarray: Morse potential evaluated at x.
"""
return D_e * (1 - np.exp(-a * (x - r_e)))**2 - D_e + offset
def compute_vibrational_levels(v_levels, T_e, omega_e, omega_ex_e, D_e):
"""
Calculate vibrational energy levels using the anharmonic oscillator formula.
Parameters:
v_levels (np.ndarray): Vibrational quantum numbers.
T_e (float): Electronic term energy.
omega_e (float): Harmonic frequency.
omega_ex_e (float): Anharmonicity constant.
D_e (float): Depth of the Morse potential.
Returns:
np.ndarray: Vibrational energy levels.
"""
return T_e + omega_e * (v_levels + 0.5) - omega_ex_e * (v_levels + 0.5)**2 - D_e
def plot_electronic_levels(ax, x, ground_state, excited_state, kT, r_e):
"""Plot the ground and excited electronic energy curves."""
ground_line, = ax.plot(x, ground_state / kT, color='blue', linewidth=2, label='ground')
labelLines([ground_line], xvals=[2], zorder=2.5)
excited_line, = ax.plot(x, excited_state / kT, color='red', linewidth=2, label='excited')
labelLines([excited_line], xvals=[2], zorder=2.5)
ax.set_xlabel("Distance")
ax.set_ylabel("Energy ($k_{\\text{B}}T$)")
ax.grid(True)
ax.set_title("Electronic Levels")
def plot_vibrational_levels(ax, x, ground_state, E_v, kT, r_e):
"""Plot vibrational levels as horizontal lines and overlay the ground state potential."""
for i, energy in enumerate(E_v):
x_left, x_right = find_turning_points(x, ground_state, energy)
if None not in (x_left, x_right):
line, = ax.plot([x_left, x_right], [energy / kT, energy / kT],
color='green', label=f'{i}')
labelLines([line], xvals=[r_e], zorder=2.5)
ax.plot(x, ground_state / kT, color='blue', linewidth=2, label='Ground state')
ax.set_title('Vibrational Levels')
ax.set_xlabel("Distance")
ax.grid(True)
def plot_rotational_levels(ax, x, ground_state, E_rot_total, kT, r_e, xmin_rot, xmax_rot):
"""Plot rotational levels for the v=0 vibrational state."""
for i, energy in enumerate(E_rot_total):
x_left, x_right = find_turning_points(x, ground_state, energy)
if None not in (x_left, x_right):
rot_line, = ax.plot([x_left, x_right], [energy / kT, energy / kT],
color='purple', label=f'{i}')
labelLines([rot_line], xvals=[r_e], zorder=2.5)
ax.plot(x, ground_state / kT, color='blue', linewidth=2, label='Ground state')
ax.set_title('Rotational Levels')
ax.grid(True)
ax.set_xlim(xmin_rot, xmax_rot)
def main():
# Define distance range and thermal energy scale
xmin, xmax = 0.3, 3
x = np.linspace(xmin, xmax, 200)
kT = k * 300 / eV
# Ground-state Morse potential parameters
D_e = 4.75
a = 1.93
r_e = 0.741
ground_state = morse_potential(x, D_e, a, r_e)
# First excited state parameters (with offset)
D_e_exc = 3.582
a_exc = 2.0
r_e_exc = 1.293
offset_exc = 11.3694
excited_state = morse_potential(x, D_e_exc, a_exc, r_e_exc, offset=offset_exc)
# Create subplots using a mosaic layout
fig, axs = plt.subplot_mosaic([[0, 1, 2]], figsize=(9, 3))
plot_electronic_levels(axs[0], x, ground_state, excited_state, kT, r_e)
# Calculate vibrational energy levels
T_e = 0.0
omega_e = 0.545681 # eV
omega_ex_e = 0.015044 # eV
v_max = 5
v_levels = np.arange(v_max + 1)
E_v = compute_vibrational_levels(v_levels, T_e, omega_e, omega_ex_e, D_e)
xmin_rot, xmax_rot = 0.55, 1.0
plot_vibrational_levels(axs[1], x, ground_state, E_v, kT, r_e)
# Rotational energy levels for vibrational level v=0
B_e_cm = 60.8530
alpha_e_cm = 3.0622
D_e_cm = 0.0471
v = 0
B_v_cm = B_e_cm - alpha_e_cm * (v + 0.5)
D_v_cm = D_e_cm # same for v=0
cm_to_eV = 1.239841984e-4
B_v_eV = B_v_cm * cm_to_eV
D_v_eV = D_v_cm * cm_to_eV
J_max = 4
J_levels = np.arange(J_max + 1)
rotational_offsets = B_v_eV * J_levels * (J_levels + 1) - D_v_eV * (J_levels * (J_levels + 1))**2
E_rot_total = E_v[v] + rotational_offsets
plot_rotational_levels(axs[2], x, ground_state, E_rot_total, kT, r_e, xmin_rot, xmax_rot)
# Set axis limits for clarity
axs[0].set_xlim(xmin, xmax)
axs[1].set_xlim(xmin, 1.8)
axs[2].set_xlim(xmin_rot, xmax_rot)
axs[0].set_ylim(-200, 600)
axs[1].set_ylim(-200, -50)
axs[2].set_ylim(-174, -166)
plt.tight_layout()
glue("thermal_energy", fig, display=False)
plt.close(fig)
if __name__ == "__main__":
main()
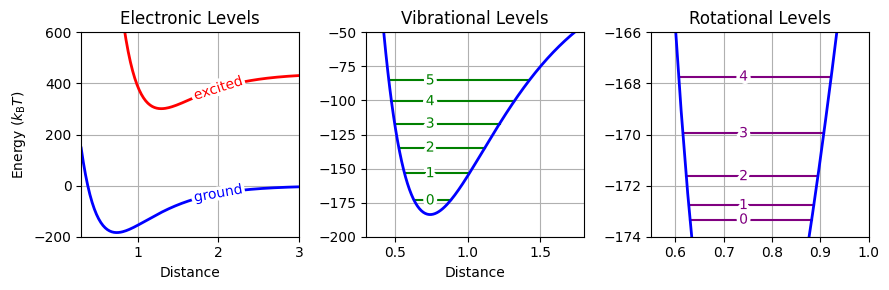
Fig. 28 Energy level diagram for a diatomic molecule at 300 K (energies scaled by kT). The first subplot shows the ground and first excited electronic potential curves, the second displays the quantized vibrational levels over the ground-state potential, and the third presents the rotational levels for the v = 0 state.#
