Chapter 24: Newton-Raphson Method#
Learning Objectives#
By the end of this lecture, you will be able to:
Understand the Newton-Raphson method.
Implement the Newton-Raphson method to find the roots of a function.
Apply the Newton-Raphson method to solve nonlinear equations.
Newton-Raphson Method#
The Newton-Raphson method is an iterative technique for finding the roots of a real-valued function \(f(x)\). The method starts with an initial guess \(x_0\) and iteratively refines the guess using the formula:
where \(f'(x_n)\) is the derivative of the function \(f(x)\) evaluated at \(x_n\). The process is repeated until the difference between successive approximations is less than a specified tolerance.
Geometric Interpretation#
The Newton-Raphson method can be interpreted geometrically as follows. Given a function \(f(x)\), the tangent line to the curve at the point \((x_n, f(x_n))\) is given by:
The intersection of this tangent line with the \(x\)-axis gives the next approximation \(x_{n+1}\):
Solving for \(x_{n+1}\), we get:
This is the same formula as the one derived algebraically.
import numpy as np
import matplotlib.pyplot as plt
# Define the function f(x) = x^3 - 2x - 5
def f(x):
return x**3 - 2*x - 5
# Define the derivative f'(x) = 3x^2 - 2
def f_prime(x):
return 3*x**2 - 2
# Define the tangent line at x = 2
def tangent_line(x):
return f_prime(2)*(x - 2) + f(2)
# Plot the function f(x) and the tangent line at x = 2
x = np.linspace(0, 4, 100)
y = f(x)
tangent = tangent_line(x)
# Calculate the next approximation using Newton-Raphson method
x_new = 2 - f(2) / f_prime(2)
# Plot the function and the tangent line
plt.figure(figsize=(8, 6))
plt.plot(x, y, label='$f(x) = x^3 - 2x - 5$')
plt.plot(x, tangent, label='Tangent line at $x = 2$')
plt.axvline(x=2, color='r', linestyle='--', label='$x_0 = 2$')
plt.axvline(x=x_new, color='g', linestyle='--', label='$x_1 = 2 - f(2)/f\'(2) = {:.1f}$'.format(x_new))
plt.xlabel('$x$')
plt.ylabel('$f(x)$')
plt.legend()
plt.grid(True)
plt.show()
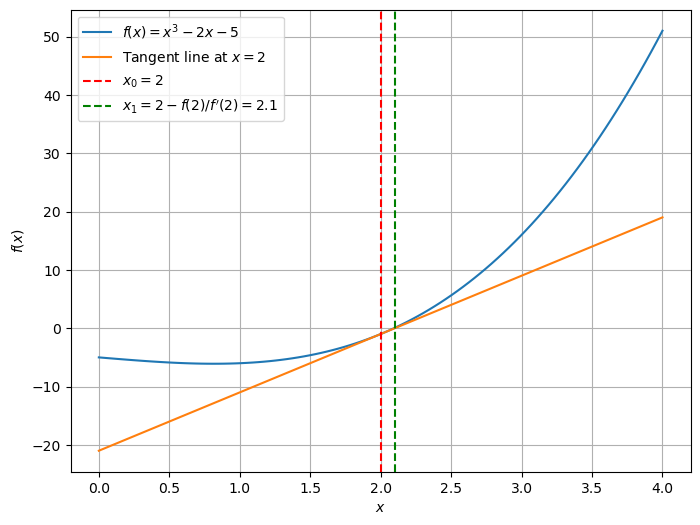
Implementation of Newton-Raphson Method#
Let’s implement the Newton-Raphson method in Python to find the root of a function \(f(x)\). We will define the function \(f(x)\) and its derivative \(f'(x)\), choose an initial guess \(x_0\), and iterate until the convergence criterion is met.
import numpy as np
def f(x):
return x**3 - 2*x - 5
def f_prime(x):
return 3*x**2 - 2
def newton_raphson(f, f_prime, x0, tol=1e-6, max_iter=100):
x = x0
for i in range(max_iter):
x_new = x - f(x) / f_prime(x)
if np.abs(x_new - x) < tol:
return x_new
x = x_new
return None
# Initial guess
x0 = 2.0
# Find the root using Newton-Raphson method
root = newton_raphson(f, f_prime, x0)
print(f"Root of the function: {root}")
Root of the function: 2.0945514815423265
In this example, we define a function \(f(x) = x^3 - 2x - 5\) and its derivative \(f'(x) = 3x^2 - 2\). We choose an initial guess \(x_0 = 2.0\) and apply the Newton-Raphson method to find the root of the function. The result is printed as the output.
Multivariate Newton-Raphson Method#
The Newton-Raphson method can be extended to find the roots of a system of nonlinear equations. Given a system of equations \(f(x) = 0\), where \(f: \mathbb{R}^n \rightarrow \mathbb{R}^n\), the Newton-Raphson method iteratively refines the guess \(x_n\) using the formula:
where \(J(x_n)\) is the Jacobian matrix of \(f(x)\) evaluated at \(x_n\). The process is repeated until the difference between successive approximations is less than a specified tolerance.
Implementation of Multivariate Newton-Raphson Method#
Let’s implement the multivariate Newton-Raphson method in Python to solve a chemical equilibrium problem. Consider a chemical system with two species, A and B, in equilibrium:
with the equilibrium constant \(K = 100\).
We aim to find the equilibrium concentrations of A (\([\text{A}]\)) and B (\([\text{B}]\)) starting from initial concentrations:
Equations to Solve#
The equilibrium constant relation:
Rearrange to:
Conservation of mass:
Rearrange to:
These form a nonlinear system of equations:
Newton-Raphson Algorithm#
Start with an initial guess:
At each iteration, compute:
where \(\mathbf{J}\) is the Jacobian matrix of partial derivatives:
Compute the partial derivatives:
So:
Iterate until convergence (when \(\|\mathbf{F}(\mathbf{x}_n)\|\) is sufficiently small).
Python Implementation#
Here’s Python code to implement this:
import numpy as np
# Define the functions
def F(x):
A, B = x
return np.array([
B**2 - 100 * A, # f1
A + B - 1.5 # f2
])
# Define the Jacobian
def J(x):
A, B = x
return np.array([
[-100, 2 * B], # Partial derivatives of f1
[1, 1] # Partial derivatives of f2
])
# Initial guess
x0 = np.array([1.0, 0.5])
# Newton-Raphson iteration
tolerance = 1e-6
max_iter = 100
for i in range(max_iter):
Fx = F(x0)
Jx = J(x0)
dx = np.linalg.solve(Jx, -Fx) # Solve J * dx = -F
x0 = x0 + dx
if np.linalg.norm(Fx, ord=2) < tolerance:
print(f"Converged in {i+1} iterations.")
break
else:
print("Did not converge.")
# Results
print(f"Equilibrium concentrations: [A] = {x0[0]:.6f}, [B] = {x0[1]:.6f}")
Converged in 4 iterations.
Equilibrium concentrations: [A] = 0.021849, [B] = 1.478151
In this code, we define the functions \(f_1([\text{A}], [\text{B}])\) and \(f_2([\text{A}], [\text{B}])\) and their Jacobian matrix \(\mathbf{J}\). We choose an initial guess \(\mathbf{x}_0 = [1.0, 0.5]\) and apply the Newton-Raphson method to solve the system of equations. The equilibrium concentrations of A and B are printed as the output. The analytical solution is \([\text{A}] = 0.02\) M and \([\text{B}] = 1.48\) M.
Summary#
In this lecture, we learned about the Newton-Raphson method for finding the roots of a function. We discussed the geometric interpretation of the method and implemented it in Python. We also extended the method to solve a system of nonlinear equations using the multivariate Newton-Raphson method.
