3. Ideal Gases#
3.1. Overview#
Ideal gases are a central model in thermodynamics. By simplifying microscopic interactions and treating molecules as non-interacting point particles, we can accurately predict many macroscopic properties for gases under appropriate conditions. This lecture reviews the classical gas laws, derives the ideal gas equation of state, and discusses the assumptions underlying the ideal gas model.
3.2. Gas Laws#
Show code cell source
import matplotlib.pyplot as plt
import numpy as np
from scipy.constants import k, N_A
from labellines import labelLines
from myst_nb import glue
# Constants
T = 290 # Temperature in Kelvin (Boyle's Law)
P = 1.0 # Fixed pressure in bar (Charles' Law)
V = 24.53 # Fixed volume in liters (Gay-Lussac's Law)
N = N_A # Number of particles for Avogadro's Law
temperatures = np.linspace(273.15, 373.15, 101) # Temperatures in Kelvin
volumes = np.linspace(1, 40, 400) # Volumes in liters
number_of_particles = np.linspace(0.1, 10, 100) * N_A
# Calculate pressures, volumes, etc., according to each law
pressures_boyle = N * k * T / volumes * 0.01
volumes_charles = (N * k / P * 0.01) * temperatures
pressures_gay_lussac = (N * k / V) * temperatures * 0.01
volumes_avogadro = (k * T / P * 0.01) * number_of_particles
def plot_law(ax, x, y, label, title, xlabel, ylabel):
line = ax.plot(x, y, "b-", label=label)
ax.set_title(title, fontsize=14)
ax.set_xlabel(xlabel, fontsize=12)
ax.set_ylabel(ylabel, fontsize=12)
ax.grid(True, linestyle="--", linewidth=0.5)
labelLines(line, zorder=2.5)
fig, axs = plt.subplots(1, 4, figsize=(12, 3))
# Boyle's Law
plot_law(axs[0], volumes, pressures_boyle, "$P = c_\\text{B} / V$", "Boyle (1662)",
"Volume (L)", "Pressure (bar)")
axs[0].text(0.1, 0.9, 'Constant $T$ & $N$', transform=axs[0].transAxes)
# Charles's Law
plot_law(axs[1], temperatures, volumes_charles, "$V = c_\\text{C} T$", "Charles (1787)",
"Temperature (K)", "Volume (L)")
axs[1].text(0.1, 0.9, 'Constant $P$ & $N$', transform=axs[1].transAxes)
# Gay-Lussac's Law
plot_law(axs[2], temperatures, pressures_gay_lussac, "$P = c_\\text{GL} T$", "Gay-Lussac (1802)",
"Temperature (K)", "Pressure (bar)")
axs[2].text(0.1, 0.9, 'Constant $V$ & $N$', transform=axs[2].transAxes)
# Avogadro's Law
plot_law(axs[3], number_of_particles / N_A, volumes_avogadro, "$V = c_\\text{A} N$", "Avogadro (1811)",
"Number of Particles ($N_\\text{A}$)", "Volume (L)")
axs[3].text(0.1, 0.9, 'Constant $P$ & $T$', transform=axs[3].transAxes)
plt.tight_layout()
glue('gas-laws', fig, display=False)
plt.close(fig)
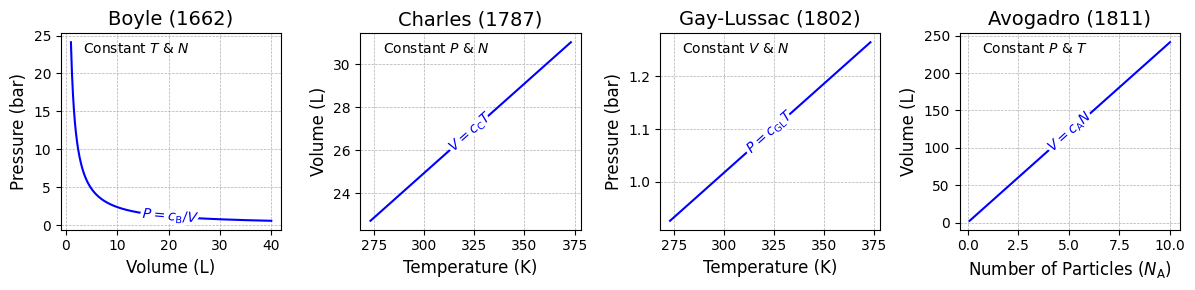
Fig. 3.1 Four classical gas laws (blue) shown in chronological order: Boyle’s law,[1] Charles’s law, Gay-Lussac’s law, and Avogadro’s law.#
All gases follow these relationships when at least one of the following conditions is met:
Pressure is relatively low,
Density is relatively low, and/or
Temperature is sufficiently high.
These conditions collectively ensure minimal intermolecular interactions, allowing the gas to behave ideally.
3.3. Deriving an Equation of State#
In Lecture 1, we defined an equation of state as a mathematical relationship among state variables. Above, each gas law relates two state variables (among \(P, V, T, N\)) under conditions where two other variables remain constant. To derive a single equation of state that relates all four variables, we can combine these laws and use multivariate calculus (as covered in Math 233).
3.3.1. Total Differential#
The total differential \(df\) of a function \(f\) of \(m\) variables \(x_1, \ldots, x_m\) is
where \(\left(\partial f / \partial x_i\right)_{\{ x_j | j \neq i \}}\) is the partial derivative of \(f\) with respect to \(x_i\), holding all other variables constant, and \(dx_i\) represents an infinitesimal change in \(x_i\).
3.3.2. Total Differential of Volume#
From Boyle’s, Charles’s, and Avogadro’s laws, we can treat \(V\) as a function of \(P, T,\) and \(N\):
Applying Equation (3.1) to \(V\):
3.3.3. Partial Derivatives via Gas Laws#
Using the gas laws in differential form, one finds:
Rearranging and employing logarithmic differentials:
3.3.4. Integrating the Total Differential#
Integrate from an initial state \((P_i, V_i, T_i, N_i)\) to a final state \((P_f, V_f, T_f, N_f)\). By properties of logarithms, we obtain
Because both initial and final states are arbitrary, the ratio \(PV / NT\) must be a constant. We thus arrive at the ideal gas equation of state:
where \(n = N / N_\text{A}\) is the number of moles and \(R = k_\text{B} N_\text{A}\) is the molar gas constant (\(R = 8.314\,\text{J mol}^{-1}\text{K}^{-1}\)).
3.4. Ideal Gas Assumptions#
A gas described by Equation (3.2) is called ideal because, under low pressures, low densities, or high temperatures, we can adopt simplifying assumptions from kinetic theory:
Particles have negligible volume (point particles).
Particles experience no intermolecular forces except during elastic collisions.
Collisions conserve total energy and momentum.
Many thermodynamic properties derive neatly from these assumptions.
3.5. Estimating Particle Distances#
Rearranging Equation (3.2), the average distance \(\langle d \rangle\) between particles is:
This simple expression shows that increasing temperature or reducing pressure increases the typical separation between gas particles.
Example: Distance Between Air Molecules at 300 K and 1 bar
Using Equation (3.3):
In air, Ar atoms (about 0.934% of air molecules) can be modeled with the Lennard-Jones potential:
At \(r = \langle d \rangle\),
which is small compared to the thermal kinetic energy,
Because \(\lvert E_\text{pot} \rvert\) is negligible relative to \(\langle E_\text{kin} \rangle\), the Ar atoms behave almost as if they are non-interacting, validating the ideal gas approximation.
3.6. Absolute Temperature Scale#
Show code cell source
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from scipy.constants import N_A
import statsmodels.api as sm
from myst_nb import glue
# Experimental data for O2 at 1 Pa:
df = pd.read_table("assets/lecture-03/isobaric-properties-for-oxygen.tsv", sep="\t").iloc[:, [0, 1, 3]]
df.columns = ["T_C", "P", "V"]
df["v"] = df["V"] * 1e27 / N_A # Convert volume to nm³/molecule
X = sm.add_constant(df["v"]) # For intercept in linear regression
y = df["T_C"]
model = sm.OLS(y, X).fit()
df["T_C_pred"] = model.predict(X)
fig, ax = plt.subplots(figsize=(4, 4))
ax.plot(df["v"], df["T_C"], "b.")
intercept, slope = model.params
line = ax.plot(df["v"], df["T_C_pred"], "r-", label=f"Slope: {slope:.2e}; Intercept: {intercept:.2f} °C")
labelLines(line, zorder=2.5)
ax.set_xlabel("Volume (nm³/molecule)")
ax.set_ylabel("Temperature (°C)")
ax.grid(True, linestyle="--", linewidth=0.5)
plt.tight_layout()
glue('absolute-temperature', fig, display=False)
plt.close(fig)
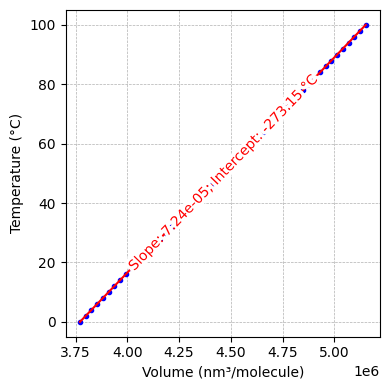
Fig. 3.2 Linear relationship between the per-molecule volume \(v\) and Celsius temperature for O₂ at 1 Pa.[2]
The red line is an ordinary least squares fit whose intercept at -273.15 °C signals the theoretical zero-volume limit, defining absolute zero (0 K).#
Charles’s law states that, at constant (low) pressure, the volume per particle is directly proportional to the gas temperature. Historically, the Celsius scale was used (\(0\,^\circ\text{C}\) as the freezing point of water and \(100\,^\circ\text{C}\) as the boiling point). However, by measuring gas volume at various Celsius temperatures and extrapolating to where volume vanishes, we identify \(-273.15\,^\circ\text{C}\) as the limit—an unphysical negative volume indicates a theoretical bound. Shifting the Celsius scale by \(273.15\) degrees places absolute zero at \(0\,\text{K}\):
This defines the Kelvin scale, an absolute temperature scale that starts at the lowest physically meaningful temperature.
