2. Kinetic Theory#
2.1. Overview#
Kinetic theory connects the microscopic motion of gas particles to macroscopic properties such as pressure and temperature. This lecture introduces the fundamental assumptions of kinetic theory, derives key equations, and highlights their physical relevance.
2.2. Foundational Assumptions of Kinetic Theory#
Large Number of Particles: A gas contains a very large number of identical particles moving randomly in all directions.
Point Particles: Each particle’s size is negligible compared to the average distance between particles.
Elastic Collisions: Collisions between particles, and between particles and the container walls, conserve both momentum and kinetic energy.
No Long-Range Interparticle Forces: Particles do not exert forces on one another except when they collide (i.e., there are no long-range attractive or repulsive forces).
Classical Mechanics Applies: Particle motion follows Newton’s second law:
\[\vec{F} = \frac{d\vec{p}}{dt},\]where \(\vec{F}\) is the net force on a particle, \(\vec{p}\) is its linear momentum, and \(t\) is time.
2.3. Deriving Pressure from Particle-Wall Collisions#
Show code cell source
import matplotlib.pyplot as plt
from myst_nb import glue
def plot_container_2d(offset=0.2):
"""Plot a 2D schematic of a gas particle in a container."""
fig, ax = plt.subplots(figsize=(12, 4))
# Dimensions
Lx, Lz = 10, 2
# Draw container
ax.plot([0, Lx, Lx, 0, 0], [0, 0, Lz, Lz, 0], color='black')
ax.fill_between([0, Lx], 0, Lz, color='lightgray')
# Gas particle
ax.plot(0.5 * Lx, 0.75 * Lz, 'o', color='blue', markersize=20, zorder=10)
ax.text(0.5 * Lx, 0.75 * Lz, "$m$", color='white',
ha='center', va='center', zorder=20, fontsize=12)
# Velocity arrows
ax.annotate("", xy=(0.5 * Lx, 0.75 * Lz), xytext=(Lx, 0.75 * Lz),
arrowprops=dict(arrowstyle="<-", color='red'))
ax.text(Lx * 2 / 3, 0.75 * Lz + offset, "$v_x$", color='red', fontsize=12, ha='center', va='center')
ax.annotate("", xy=(Lx, 0.5 * Lz), xytext=(0, 0.5 * Lz),
arrowprops=dict(arrowstyle="<-", color='red'))
ax.text(Lx * 5 / 6, 0.5 * Lz + offset, "$-v_x$", color='red', fontsize=12, ha='center', va='center')
ax.annotate("", xy=(0, 0.25 * Lz), xytext=(0.5 * Lx, 0.25 * Lz),
arrowprops=dict(arrowstyle="<-", color='red'))
ax.text(0.25 * Lx, 0.25 * Lz + offset, "$v_z$", color='red', fontsize=12, ha='center', va='center')
# Length indicators
ax.annotate("", xy=(0, -offset), xytext=(Lx, -offset),
arrowprops=dict(arrowstyle="<->", color='black'))
ax.text(Lx / 2, -2 * offset, "$L_x$", color='black', fontsize=12, ha='center', va='center')
ax.annotate("", xy=(-offset, 0), xytext=(-offset, Lz),
arrowprops=dict(arrowstyle="<->", color='black'))
ax.text(-2 * offset, Lz / 2, "$L_z$", color='black', fontsize=12, ha='center', va='center')
ax.set_xlim(-1, Lx+1)
ax.set_ylim(-1, Lz+1)
ax.axis('off')
return fig
fig = plot_container_2d()
glue('gas-in-container', fig, display=False)
plt.close(fig)
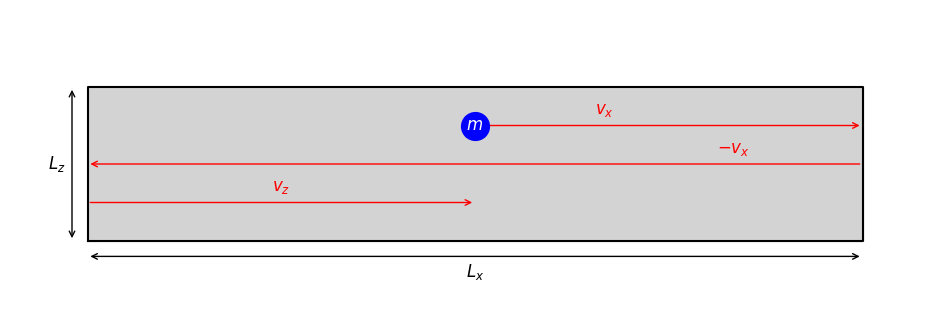
Fig. 2.1 A two-dimensional representation of a single gas particle in a cuboid container (gray). Velocity components are shown in red. The length \(L_y\) is not depicted, as it extends perpendicular to the plane of view.#
2.3.1. Microscopic Picture of Pressure#
Pressure is the force exerted per unit area on the container walls. On a microscopic level, this force comes from the collective effect of countless collisions of gas particles with the walls.
2.3.1.1. Particle Momentum Change#
For an elastic collision of a particle of mass \(m\) moving with velocity \(v_x\) in the \(x\)-direction, the momentum change is:
2.3.1.2. Time Between Collisions#
If the container has length \(L_x\) in the \(x\)-direction, the time between two consecutive collisions of the same particle with that wall is:
2.3.1.3. Force on the Wall#
A single particle’s average force on the wall (in the \(x\)-direction) is then:
2.3.2. Total Pressure#
For \(N\) identical particles with isotropic motion in a volume \(V\), the total pressure \(P\) is:
where \(v_i\) is the speed of the \(i\)-th particle. Using the average speed squared \(\langle v^2 \rangle\), we get:
This equation shows how the macroscopic pressure depends on the microscopic speeds of the particles.
2.4. Kinetic Energy and Temperature#
The average translational kinetic energy per particle is:
From the ideal gas law \(P V = N k_\text{B} T\) (to be discussed in more detail in Lecture 3), one can show that
where \(k_\text{B}\) is the Boltzmann constant and \(T\) is the absolute temperature. This result—called the equipartition theorem—indicates that the temperature is directly proportional to the average kinetic energy of the particles.
2.5. Estimating Particle Speeds#
By rearranging Equation (2.2), we obtain the root-mean-square (rms) speed:
This expression shows that:
Hotter gases (larger \(T\)) have faster particles.
For a given temperature, lighter particles (smaller \(m\)) move faster than heavier ones.
Example: Speed of Air Molecules at Room Temperature
Air is roughly 78% nitrogen (N\(_2\)) by volume. Thus, a good estimate for the speed of air molecules at around 300 K is the rms speed of an N\(_2\) molecule at 300 K.
Using the molar mass of N\(_2\), \(M_\text{r} = 28.0134\,\text{g/mol}\),[1] one finds:
This speed is significantly faster than a Boeing 747-8 airliner at cruising velocity (about 660 mph).[2]
